The Physics Behind Swimming

The Physics Behind Swimming

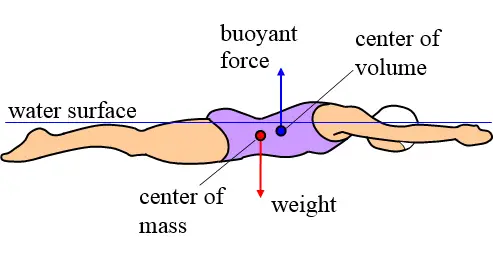
Swimming is both a recreational and competitive sport that involves some type of relationship of forces between the water and the swimmer. Swimmers must push against the water to be able to move through it. For a swimmer, or any object in general, to float, it must be less dense than the water so the buoyancy force can lift the object. The theory behind this lifting of an object is called Archimedes' Principle, which states that any object that is suspended in a fluid is acted upon by an upward buoyant force equal to the weight of the fluid that is displaced by the object. This means that when an object is floating, the part of the object that lies below the surface displaces a water weight equal to the weight of the object. This weight is equal to the buoyant force pushing upward on the object. The point at which the object weight is equal to the buoyant force pushing upwards on the object shows the correspondence between the equilibrium point and the amount that the object sinks below the surface. Also, the buoyant force acts through the center of buoyancy, which is the center of the immersed part of the object, or the volume of water displaced by the object. For the object to be able to maintain its orientation in the water, the buoyant force must pass through the center of mass of the object.

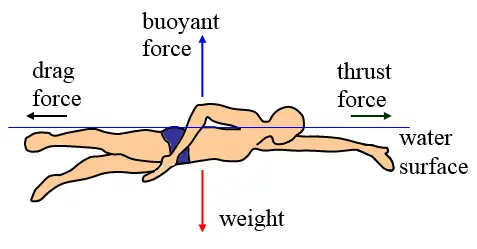
A swimmer moving through the water had four basic forces acting upon them.

By moving their arms and legs through the water, the swimmer creates a thrust force that propels them through the water. For a swimmer moving at constant speed, the thrust force is equal to the drag force. The drag force of a swimmer is created by the motion of the swimmer. This force of drag directly resists the motion of the swimmer, and this force exists any time an object moves through a fluid. The faster a swimmer moves through the water, the greater the drag force. This is the equation to calculate the force of drag when swimming:

ρ = density of the water (fixed variable)

A = cross sectional area (underwater profile of swimmer)

C = drag coefficient (how water interacts with the object)

v = velocity of the swimmer (speed)

Example problem:

The density of water = 1 g/cm³ and the addition of the chlorine adds such a minuscule amount to the density that it stays the same in this problem

A = 9.517 (calculated from the height and weight of the swimmer)

C = .92 (average value for a fast female swimming freestyle, the fastest stroke of the four used)

v =  1.64 m/s (calculated from Vavg = Δ x / Δ t for the average female 100m freestyle)

so, Fdrag = 11.7746 for this example problem

There are three basic components to the drag force:

1.) Pressure (Form) Drag - due to the swimmer "pushing" the water out of the way when swimming

2.) Skin Friction Drag - due to the friction between the water and the swimmer's body as water flows

(This type of drag occurs inside a very thin layer of water directly touching the swimmer's body)

3.) Wave Drag - due to the surface waves produced by the swimmer moving

There are special suits produced by companies that try to reduce drag of swimmers, thus allowing them to move faster.

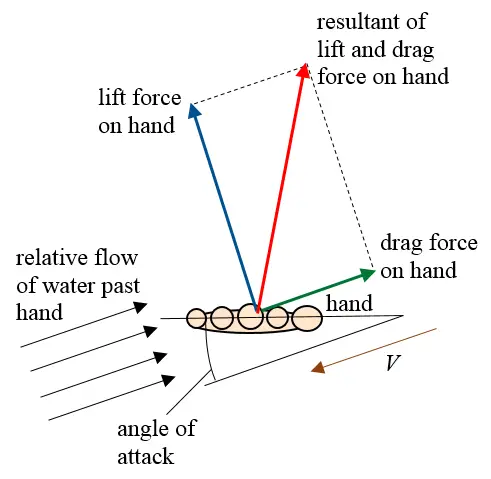
The hands of a swimmer are a very controllable thrust force in the technique and can be optimized for the best performance of a swimmer. The hands of a swimmer moving through the water almost mimic an airplane wing moving through the air.

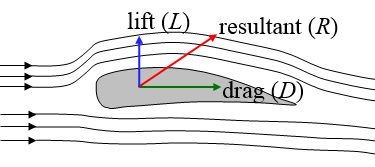
The forces acting upon the hand can be broken down into a drag force and a lift force. The drag force acts in the same direction as the (oncoming) flow velocity. The lift force acts perpendicular to the flow velocity and points in the direction of inclination of the hand, relative to the flow velocity. The amount of inclination of the hand is observed by the angle of attack, which relates to the magnitude of the lift force and drag force. The vector sum of the lift and drag forces is the actual force that acts on the hand as it moves through the water a a certain velocity. Swimmers use many complicated hand motions to generate the greatest thrust possible. In the following image, D = drag force, L = lift force, and R = resultant force action on the hand of the swimmer.

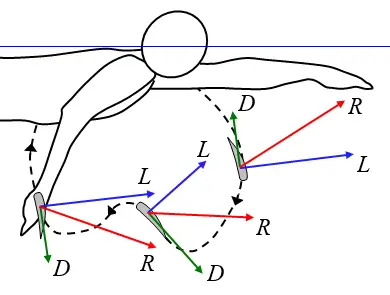
As the swimmer moves their hand along the optimal path shown, and adjusting the position and orientation of the hand as needed, the swimmer is able to maximize the resultant force and keep it pointing forward in the goal direction. This process has to do with each swimmer's "feel" for the water, which allows them to be able to use their hands to their advantage. The hand of a swimmer is represented by a wing, which experiences the forces as shown below.

The forces acting on the hand are proportional to the square of the velocity of the object relative to the fluid. The greatest forces on the hand are exerted on the part of it that moves the fastest through the water. The cylindrical shape of the forearm and upper arm of a swimmer make them unable to experience a significant lift force no matter their orientation. This also means that the drag force experienced by the forearm and upper arm will always be too low to produce any significant force.

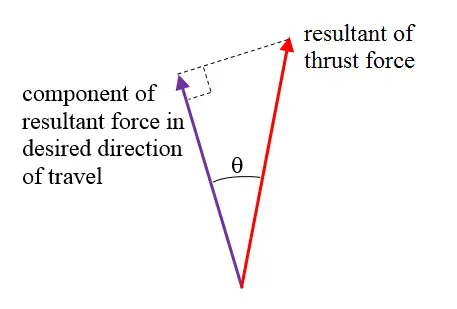
The goal of a competitive swimmer is to point the resultant thrust force in the desired direction of motion as much is physically possible for that person. The part of the resultant force that is used to propel the swimmer in the desired direction is the component force.

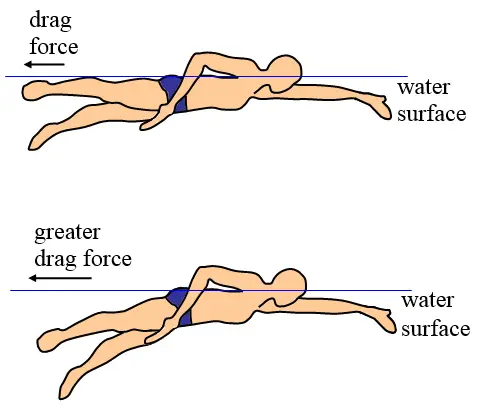
If the swimmer can keep the angle, theta, as small as possible, the amount of force used to propel the swimmer will be maximized and used to the advantage of the swimmer. In addition to trying to maximize the thrust force that propels them forward, a swimmer also wants to minimize the drag force that their body experiences. The most efficient way for a swimmer to do this is to keep their body as straight as possible in the direction of travel, becoming almost aerodynamic. This shift of the body minimizes pressure drag by minimizing the frontal area in the direction of motion.

The drag force that a swimmer wishes to minimize is that resisting the movement of their body through the water.

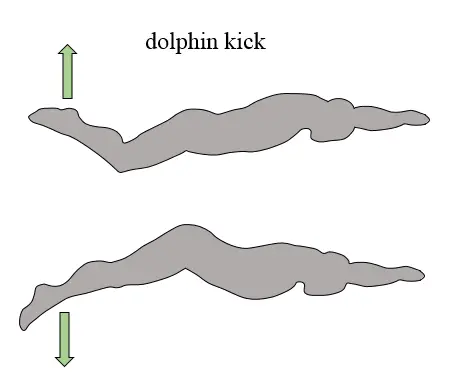
In competitive swimming, a certain kind of underwater kick, a dolphin kick, is used when leaving every wall to maximize the speed of a swimmer after pushing off and gaining momentum. Swimming underwater using the dolphin kick is much more efficient, and much faster, than swimming at the surface of the water because there sone less source of drag present, this is the wave drag that is only generated when moving at the surface. The most elite swimmers have the ability to propel themselves at up to 2.5 m/s underwater using this kick. The top surface speeds reached by elite swimmers are barely comparable to this speed.

The undulating motion of the swimmer in this dolphin kick "pushes" back on the water, and creates a thrust, using a wave-like motion. Due to Newton's third law, the water pushes back on the swimmer, creating a thrust propelling the swimmer forward. This action-reaction mechanics at work in this instance involves the creation of swirling vortices around the swimmer, which is the physics taking place. This form of physics involves the frequent use of Computational Fluid Dynamics to understand the complexity of the interaction between the swimmer's body and the water.

The physics behind swimming that has been found through this research relates to me personally because I am a swimmer and I use many of these techniques, such as reduction of drag, hand placement, and dolphin kick, to help me go faster when I am competing. I am able to understand the reasoning for many methods to go faster. This research has also helped me learn a lot about how each component of swimming relates to each other and how to better my performances even more. Thinking about my sport in a scientific way has shown me things I never knew about something I have done for over ten years.

Citations

Allain, Rhett. “Wanna Swim Like Phelps? Take a Dive Into the Physics of Drag.” Wired, Conde Nast, 3 June 2017, www.wired.com/2016/08/wanna-swim-like-ledecky-take-dive-physics-drag/.

“Physics Of Swimming.” Real World Physics Problems, www.real-world-physics-problems.com/physics-of-swimming.html.