The Physics Behind The Perfect Rocket Launch

Rocket Physics!

Rocket physics, in the most basic sense, involves the application of Newton's Three Laws of motion to a system that has a variable mass. A rocket has variable mass as a result of its fuel burning off during the course of the flight. There are many factors that must be considered in order to achieve a perfect launch. These factors include Earth's rotation, air resistance, the propellants specific energy, and maximum acceleration tolerable by the specific payload it is carrying. However, for this article, it will be easier to assume this rocket is not connecting to a satellite and is simply traveling into deep space.  

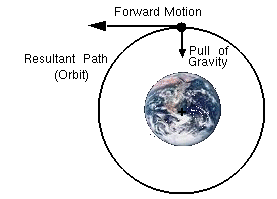
To enable a rocket to climb into low Earth orbit, it is necessary to achieve a speed over 40,250 km per hour, which is called escape velocity. This specific velocity enables a rocket to leave Earth and travel out into deep space. 

Newton's Laws of Motion:

1. Objects at rest will stay at rest and objects in motion will stay in motion in a straight line unless acted upon by an unbalanced force.
2. Force is equal to mass times acceleration.
3. For every action there is always an opposite and equal reaction.

             

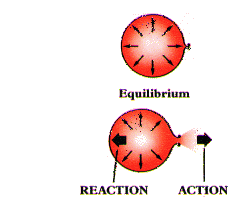
Forces to consider:

The equations of Motion - the basis of Rocket Physics:

The two stages below show the vertical acceleration of a rocket. The intended purpose of the two stages is to show the state of the system at "t" and "t+dt".  Variable t is time and time t+dt, where dt is a very small time step.

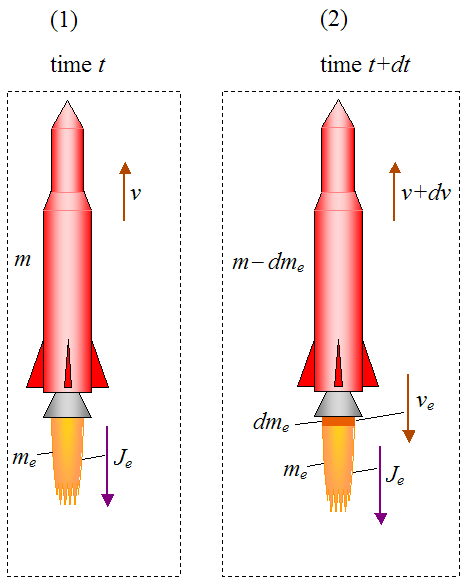
In the diagram above, 

m is the mass of the rocket (including propellant), at stage 1

m_e is the total mass of the rocket exhaust (that has already exited the rocket), at stage 1 

v is the velocity of the rocket, at stage 1 

J_e is the linear momentum of the rocket exhaust (that has already exited the rocket), at stage (1). This remains constant between 1 and 2 

dm_e is the mass of rocket propellant that has exited the rocket (in the form of exhaust), between 1 and 2

dv is the change in velocity of the rocket, between 1 and 2

v_e is the velocity of the exhaust exiting the rocket, at stage 1

Using calculus to derive the equation, it looks like this. ΣF_y is the sum of the external forces in the vertical direction acting on all the particles in the system

The simplified version of the equation above looks like this:

Staging:

With a very limited and quick burning fuel supply, all modern rockets use staging in order to shed unnecessary or dead weight. Once all the fuel is consumed the early stages, the are shed. This allows for maximum acceleration for the payload the rocket is carrying, as previously states. 

Conclusion:

Rocket physics is a complex and meticulous process that requires the consideration of many factors that need to be accounted for in an equation. If even one factor is not taken into consideration, such as an error in staging or fuel tanks, it can have detrimental effects. This was seen with the Challenger Shuttle Disaster which took the lives of all of its crew members. Note that not all of the factors required for a flawless launch were explained. Rocket science is an art and couldn't be fully explained in this short blog. 

Sources: 

https://www.grc.nasa.gov/WWW/k-12/rocket/TRCRocket/rocket_principles.html

https://www.real-world-physics-problems.com/rocket-physics.html

http://ffden-2.phys.uaf.edu/211.fall2000.web.projects/I.%20Brewster/physics.html

https://brilliant.org/wiki/rocket-physics/