Skip to main content

Blog #3: Effect of a track's curve on running times

The sport of track and field, regardless of whether it is inside or outside, consists of three generally accepted disciplines, sprinting, distance and throwing. Sprinters in particular are attempting to go as fast as possible over short distances and due to this the shape of a track affects these athletes the most. A standard track compliant to International Association of Athletics Federations regulations will consist of a rectangle with a semi circle at each end (as seen below).  The straight-aways on a track are 84.39 meters long while the semi-circles have a radius of 36.5 meters making each semi circle have a circumference of 114.7 meters roughly equaling a distance of 400 meters. For very short sprint events like the 100 meters, the entire race is contained to one straightway making it very easy for these sprinters to hit their max speed. Put the same sprinters into a longer race like the 200 meters or 400 meters, and those sprinters run slower not just because of the longer distance but also the very shape of the track which forces them to run around a corner. While rounding the corner, a sprinter is forced to slow down due to the forces acting on them, this is why sprinters frequently complain that the inside lane is too tight
The physics behind running on the curve of a track is quite interesting as runners are producing forces which counteract the forces acting on them. The runner must produce a centriptal force to stay on the track which can be defined as Fc= -mass * speed^2/radius of turn. The speed is the tangental speed of the runner, mass is the mass of the runner and the nagative sign comes from the fact the force is directed towards the center of track. The tighter the turn the more force or less speed is neccesary to succesfully make the turn. This force is limited by the amount of friction acting between the shoe and the track's surface. The force of friction if f=μ*normal force with μ being the coefficent of friction while the runner is in contact with the rack. If the track is flat this normal force is the weight of runner and if the friction is low the runner can lose contact with the service and fly off the curve. 

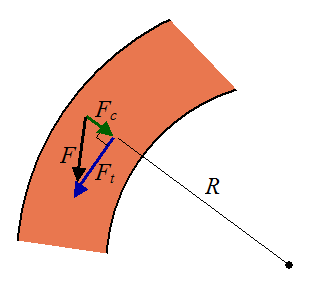
 In the above picture, the turn radius is depicted as R, the centrifugal force needed to maintain a path around the track is Fc, the force neccesary to propel the runner along the track is Ft and the total force exerted by the runner on the track is F. Using an equation from my sources, f(t) -(v/τ)=dv(t)/dt, I can begin to solve how much slower a race is when it is run around a curved track. This earlier equation can be rewritten as dv(t)/dt + (v/τ) = f since f(t)=f. This equation is a straight line motion of a runner on the straight part of a track with the f point in the direction of the motion of the runner. Referring the earlier photo, it can be determined that v(t) is in the tangental direction. The right side of the equation must be replaced with ft/m as it must be applied to the tangental direction, creating dv(t)/dt + (v/τ) = Ft/m. From here the equation can be solved:

From here f/m = f and fc/m = v^2/R

Finally the equation becomes

For a 200 meter race, the starts are staggered so that every runner runs exactly 100 meters of the race on the curve. The radius of the curve of each lane is very different but by knowing that a lane is 1.22 meters wide the inner radius of any lane n would be   


The solving of this equation requires the expansion of the equation to a point I do not quite understand which can be seen in Igor Alexandrov and Philip Lucht's journal article in the American Journal of Physics. In the end, a runner in the innermost lane (lane 1) would run the 200 meters in 19.72 seconds while the runner in lane 8 would run in 19.6 seconds creating a big time difference causing almost a full meter of seperation between the two runners which is quite big at the college level and beyond. Sadly however, runners in lane 8 do not win as often as the math says as they have psychological disadvantage as they can not see the position of the other runners until the final stretch. 

Sources

Joseph B. Keller, A Theory of Competitive Running, Physics Today 26(9), 42-47 (1973). http://eaton.math.rpi.edu/CourseMaterials/Fall01/AK6600/run2.pdf

J. Strnad, Physics of Long-Distance Running, American Journal of Physics 53, 371- 373 (1985). http://aapt.scitation.org/doi/abs/10.1119/1.14169

Igor Alexandrov and Philip Lucht, Physics of Sprinting, American Journal of Physics 49, 254-257 (1981). https://www.researchgate.net/publication/243489558_Physics_of_sprinting

https://healthfully.com/dimensions-running-track-8232920.html   

http://www.madsci.org/posts/archives/2001-05/989942384.Ph.r.html


Comments

Post a Comment

Popular posts from this blog

Physics Behind Drone Flight

A drone flies by using its downward thrust and forcing air in a particular direction in order to sustain a certain speed as well as a specific height. In this video my friend and I had been flying a drone at exactly 4 mph which converts to 1.788 m/s. In this project, we will be determining the forces acting upon the drone in order to sustain a consistent flight in terms of velocity and height while excluding the effects of air resitance. The drone is flying at an angle of 28˚, this is found by extending the tilted axis of the drone to the horizontal and finding the angle with a protractor. From this angle we will be able to calculate the downward thrust and the acceleration of the drone that allows it to maintain its height and velocity during flight. When the mass of the drone is taken it results in 734 grams or .734 kilograms, which will also be used for the calculations within the project. The freebody diagram pictured above will alow us to derive the force equations f...
Post a Comment
Read more

Physics of Black Holes...Or Lack Thereof

Isabella Jacavone To comprehend how the universe works, we must dwell into the most basic building blocks of existence; matter, energy, space, and time. NASA's  Physics of the Cosmos program involves cosmology, astrophysics, and fundamental physics intended to answer questions about the elusiveness of complex concepts such as black holes, neutron stars, dark energy, and gravitational waves. In this blog post, I'd like to elaborate on a subject that is very intriguing  to me; Black holes. And more specifically, what would happen if we got near one. A black hole is anything but a hole, but rather an immense amount of matter compacted into an extremely small area. A black hole is caused when, hypothetically, a star four times more massive than our sun collapses into a sphere no bigger than 600 square km. To put that in perspective, that's about the size of New York City. B lack holes were predicted by Einstein's theory of general relativity, which showed that when a...
Post a Comment
Read more

Aerodynamics of a Golf Ball

One may wonder how a small golf ball can travel at incredibly high speeds for such long distances.  While the swing of the club is a major component, the structure of the golf ball is quite important.  Unlike a baseball or tennis ball, a golf ball has dimples all over it (usually 336 dimples).  These dimples allow the golf ball to travel without facing much air resistance.  This diagram shows how air travels around the golf ball. The dimples on the golf ball also prevent drag that would occur in the wake region, resulting in further distance.  Also due to the contact with the club during the swing, the golf ball has backspin during its entire flight.  This diagram shows the motion of the golf ball mid flight with the lift force of F. There are hundreds of different types of golf balls that a player can choose.  Some show little affect to a player's game while others can alter their performance completely.  Personally, I prefer Callaway Supers...
Post a Comment
Read more